We have been doing fractions for the past two weeks... Mainly trying to get the students to understand what halves and quarters are, then moving them onto understanding that half a half is a quarter, so two quarters is the same as one half etc. Only two of the students in my class can independently find multiple parts of a whole, (e.g. 3/4, 5/6). The rest are still finding one of (e.g. 1/3, 1/4, 1/2)
In a one hour session today, I helped move three of my lower achieving students up in the strategy they use and how they express their thinking.
We started with this... (which was irrelevant to our question, but that is besides the point.) The point is he couldn't explain verbally, visually or anyway how he got his answer.
I explained to them how with fractions, the bottom number is how many groups you have. We practiced splitting numbers into groups and that the top number is how many groups you are looking at. For example, half of ten means you put ten into two groups (because the bottom number is 2) then look at how many are in one group (because the top number is a 1).
I started giving the students fraction word problems about 1/4, 1/2, 1/3 and they were getting it and could draw their thinking, and then talk about what they drew as a way of explaining how to get their answer.
Our question here was -
'Dad has 20 cookies and gives 1/4 to each of his 3 children. The rest he gives to mum. How many cookies did mum get?
Notice how they have drawn four squares, (which shows me they understand that for quarters you need 4 groups), put dots in each box to represent the cookies (which shows me they understand how to share things equally), circled one box (which shows me they understand they are looking for ONE quarter, rather than two or three quarters) and written the number of cookies mum gets next to their drawing (which shows me they can find part of a whole).
How much learning can be seen in one snapshot of a students drawing is amazing isn't it...
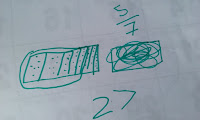
They seemed to find quarters, halves and thirds easy by using this strategy, so I upped the anti and gave them fractions even the rest of the class hadn't seen yet. Sixths, sevenths, tenths etc, and asked them to find multiple parts.
I gave the students variations of this word problem
'Miss Ashley has (X) number of lollies and gave (fraction) to the green table. How many lollies did she give them?'
Here is their thinking...
(K, C and L are the students initials, to protect their identity.)
 K - Miss Ashley has 20 lollies and gave 2/4 to the green table. How many lollies did she give them? Also seen here on the left side is the answer to 'Miss Ashley has 30 of lollies and gave 1/3 to the green table. How many lollies did she give them?'
K - Miss Ashley has 20 lollies and gave 2/4 to the green table. How many lollies did she give them? Also seen here on the left side is the answer to 'Miss Ashley has 30 of lollies and gave 1/3 to the green table. How many lollies did she give them?' L - Miss Ashley has 50 lollies and gave 9/10 to the green table. How many lollies did she give them?
L - Miss Ashley has 50 lollies and gave 9/10 to the green table. How many lollies did she give them? L - Miss Ashley has 30 lollies and gave 8/10 to the green table. How many lollies did she give them?
L - Miss Ashley has 30 lollies and gave 8/10 to the green table. How many lollies did she give them? C - Miss Ashley has 30 lollies and gave 2/10 to the green table. How many lollies did she give them?
C - Miss Ashley has 30 lollies and gave 2/10 to the green table. How many lollies did she give them?
They went from barely knowing what halves and quarters were, to being able to find 9/10 and 5/7 of a number. Incredible! I was so proud of them for stepping up such a HUGE amount during one hour of intensive teaching, and I could see they were buzzing and were proud of themselves as well. They were actually sad to pack up for morning tea!







No comments:
Post a Comment
Thank you for leaving me feedback!